شبیه سازی مونت کارلو
فرض کنید X1…Xn متغیرهای تصادفی مستقل و همتوزیع (i.i.d) با تابع توزیع تجمعی معلوم F وT آماره (برآوردگر) مورد نظر باشد. با استفاده از شبیه سازی مونت کارلو می توان توزیع، اریبی، خطای معیار و …T را بصورت مراحل زیر تقریب کرد .
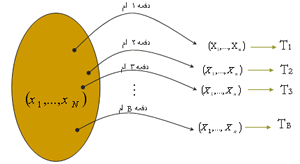
مرحله ۱- نمونه تصادفی مستقل و همتوزیع از توزیع F بدست می آید.
مرحله ۲ – آماره T بر روی نمونه مرحله ۱ بصورت T ( T1…Tn ) می گردد.
مرحله ۳ – مراحل ۱ و ۲ را B بار تکرار می شود .
-) برای B های بزرگ تابع توزیع، اریبی و خطای معیار T به صورت زیر است :
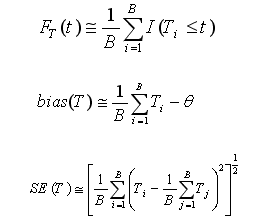
مثال کاربردی :
به منظور درک بهتر شبیه سازی مونت کارلو مثال ارائه می گردد.
مثال- در یک فرایند تحقیقاتی به منظور بدست آوردن وزن تقریبی محصول هندوانه یک مزرعه با جامعه ای نامحدود روبرو هستیم ولی این نکته را می دانیم که وزن هندوانه ها از توزیع نرمال با متوسط وزن ۶ کیلو گرم و انحراف معیار۳ کیلوگرم پیروی می کند .
اکنون سه مرحله الگوریتم مونت کارلو را در اینجا اجرا می شود :
مرحله۱- نمونه ای تصادفی به حجم ۲۵ از توزیع نرمال با میانگین ۶ و واریانس ۹ با استفاده از نرم افزار “اس پلاس” تولید می شود.به عنوان مثال ۶٫۸۸ و ۹٫۰۸ و۹٫۵۹ و۵٫۸۲ و ۲٫۳۰ و ۳٫۷۵ و ۶٫۷۹ و ۱۴٫۸۷ و ۱٫۷۲و ۵٫۳۳ و۴٫۷۳ و۱۴٫۶۳ ۵٫۲۹ و۴٫۰۹ و۵٫۸۵ و۸٫۱۶ و۵٫۷۷ و۶٫۵۲ و۲٫۶۷ و۲٫۹۲ و۰٫۲۴- و ۳٫۴۲و ۱٫۰۷و ۴٫۴۹ و۵٫۷۵ )
مرحله۲ – آماره T بر روی نمونه مرحله ۱ بصورت T ( T1…Tn ) می گردد. که در اینجا به عنوان مثال میانگین را برآورد کرده :
X = ۰٫۶۵
مرحله ۳- مراحل ۱ و ۲ را B (10000بار) تکرار می شود و
X1, … ,X ۱۰۰۰
بدست می آید. که اریبی، خطای معیار و توزیع برآوردگر بالا به صورت زیربرآورد می شود :
bias ( X ) = ۰٫۰۰۰
SE ( X ) = ۰٫۶۱۱
بافتنگار زیر توزیع X را بر اساس موارد بالا نشان می دهد :
